平面是几何学中一个重要的概念,它在我们日常生活和数学研究中都扮演着重要的角色。了解平面的基本性质对于理解几何学的许多概念和定理至关重要。本文将详细讲解平面的基本性质,帮助读者更好地理解和应用几何学知识。

平面的定义及特点
平面是指由无数条直线组成的二维空间,它没有厚度和边界。平面可以通过至少三个不共线的点来确定,这些点在平面上任意取得位置。平面上的点可以用坐标表示,使得我们能够准确地描述和计算平面上的几何性质。
平面的方向和位置关系
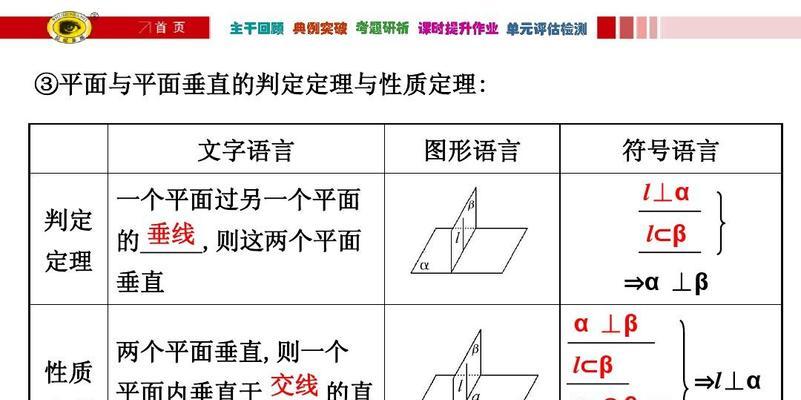
平面可以在空间中以不同的方向存在,常见的有水平平面、垂直平面和倾斜平面。平面之间可以相互平行、相交或重合。两个平面如果没有任何公共点,则它们是平行的;如果两个平面有一条或多条公共线,则它们是相交的;如果两个平面完全重合,则它们是重合的。
平面的旋转和平移
平面可以在空间中进行旋转和平移。旋转是指平面围绕一个中心点旋转一定角度,而平移则是指整个平面沿着一个方向移动一定距离。这些操作能够改变平面上图形的位置和方向,但不能改变平面的本质性质。
平面上的图形
平面上可以绘制各种几何图形,如点、线段、直线、角等。这些图形在平面上具有特定的位置和关系,可以通过几何学的原理和公式进行计算和推导。平面上的图形可以相互作用,形成各种形状和结构,从而产生丰富的几何学现象。
平面与直线的关系
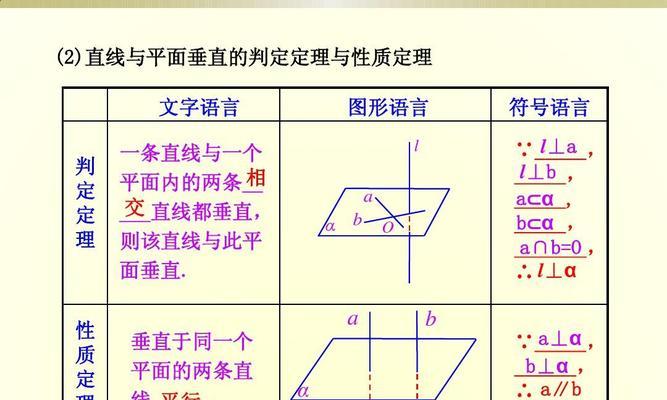
平面和直线是几何学中最基本的元素之一,它们之间存在着密切的联系。平面可以包含直线,也可以与直线相交或平行。两个平行的直线在同一个平面上,而两个相交的直线则确定一个平面。通过研究平面与直线的关系,可以推导出许多重要的几何学定理和性质。
平面的投影
当一个立体图形在平面上投影时,我们可以得到该图形在平面上的影子,这个过程称为投影。平面上的投影可以用来研究立体图形的形状、大小和位置。根据投影的特点,我们可以还原出原始的立体图形,并推断出其几何性质。
平面的对称性
平面具有许多对称性质,如镜像对称、中心对称等。镜像对称是指平面上的一点关于某条直线的镜像位置与原点关于该直线对称;中心对称是指平面上的一点关于某个中心点的镜像位置与原点关于该中心点对称。通过对称性质,我们可以推导出许多图形和结构的特殊性质。
平面上的距离和角度
在平面上,我们可以通过距离和角度来描述点、线段和直线之间的关系。距离是指两个点之间的长度,可以通过勾股定理等方法计算。角度是指两条直线之间的夹角,可以通过三角函数等方法计算。距离和角度是几何学中重要的度量方式。
平面与立体几何
平面和立体几何有着密切的联系。平面是立体几何中的一个特殊情况,立体几何可以通过截取、平行、相交等操作来构造平面。平面上的性质和定理也可以应用到立体几何中,帮助我们理解和推导立体图形的性质。
平面与解析几何
平面和解析几何有着紧密的关系。解析几何通过坐标系来描述和计算平面上的点和图形,使得我们能够利用代数的方法研究几何学问题。平面上的直线、距离和角度等概念都可以通过解析几何的方法进行分析和计算。
平面的应用领域
平面的性质和定理在许多领域有着广泛的应用,如建筑设计、地理测量、计算机图形学等。平面的概念不仅在数学研究中起到重要作用,也在实际生活中有着丰富的应用场景。
平面的发展历程
平面作为一个概念和研究对象,在历史上经历了漫长而丰富的发展过程。从古希腊数学家到现代几何学的建立,人们对于平面的认识不断深化和拓展。了解平面的发展历程可以帮助我们更好地理解和应用平面的基本性质。
平面的未解之谜
尽管人们对平面有着深入的研究,但仍然存在一些有关平面的未解之谜。例如,平面的无限性质和连续性如何理解?平面上的无穷点和无穷直线之间的关系是什么?这些问题仍然是几何学研究的热点和挑战。
平面学习的方法和技巧
学习平面的基本性质需要一定的方法和技巧。例如,通过几何画图来帮助理解和推导平面上的图形和性质;通过解析几何和数学公式来计算平面上的距离和角度等。了解这些方法和技巧可以提高我们对平面的理解和应用能力。
平面作为几何学中的基本概念,具有丰富的性质和应用。通过本文的介绍,我们了解了平面的定义、特点、方向、图形、关系等基本性质,以及与立体几何和解析几何的关系。希望读者能够从中受益,深入理解和掌握平面的基本性质,为进一步的几何学研究和实际应用奠定基础。